
Isi kandungan:
- Pengarang John Day [email protected].
- Public 2024-01-30 11:07.
- Diubah suai terakhir 2025-06-01 06:10.

Matematik, bagi kebanyakan anda, nampaknya tidak berguna. Yang paling biasa digunakan dalam kehidupan seharian kita hanyalah menambah, mengurangkan, membiak dan membahagi. Walau bagaimanapun, sangat berbeza jika anda dapat membuat dengan program. Semakin banyak anda tahu, hasil yang lebih menarik akan anda perolehi.
Langkah 1: Pergerakan & Fungsi
Izinkan saya menunjukkan beberapa gambar yang tidak diketahui untuk merangsang selera anda.
Apakah ini? Sekarang teruskan soalan ini terlebih dahulu dan terakhir anda akan mengetahui dan menggunakannya.
Pada bab terakhir, kami telah mempelajari pengaturan fungsi dan fungsi, yang dapat menjadikan grafik statik menjadi dinamis. Walau bagaimanapun, format pergerakan ini terlalu mudah. Kami akan menggunakan pengetahuan fungsi yang kami kuasai sebelumnya untuk menjalankan grafik kami dengan watak mereka sendiri.
Berapa banyak fungsi yang dapat anda kenali dari gambar di atas? Apa hubungan mereka dengan pergerakan? Sekarang mari kita pilih fungsi kuadratik daripadanya, tambahkan beberapa parameter secara rawak dan lihat apa yang akan berlaku. Contohnya, y = x² / 100.
Inilah rupa fungsi gambar. Salin kod di bawah.
[cceN_cpp tema = "fajar"] terapung x, y; batal persediaan () {saiz (300, 300); latar belakang (0); x = 0; } undian tidak sah () {stroke (255); berat badan (2); y = pow (x, 2) / 100.0; // Fungsi pow akan kembali ke kekuatan nombor sebilangan. (x, 2) mewakili segiempat sama x. Parameter pertama adalah nombor asas dan yang kedua adalah indeks. titik (x, y); x ++; } [/cceN_cpp]
Kesan Berjalan
Seterusnya, pilih sin function. Formula: y = 150 + sin (x).
Salin kod berikut.
[cceN_cpp tema = "fajar"] terapung x, y; batal persediaan () {saiz (300, 300); latar belakang (0); x = 0; } undian tidak sah () {y = tinggi / 2 + sin (radian (x)) * 150; // Fungsi radian mengubah x menjadi sudut. x ++; strok (255); berat badan (2); titik (x, y); } [/cceN_cpp]
Kesan Berjalan
Inilah grafik yang kami dapat setelah mengendalikan kod. Dan itulah jejak pergerakan mereka. Berbanding dengan yang sebelumnya, hasilnya jelas. Imej fungsi sebenarnya sesuai dengan trek pergerakan! Ia cukup sederhana. Anda hanya perlu mengganti nilai x, y menjadi koordinat. Trek bekas yang kami lukis adalah setara dengan grafik fungsi y = x² / 100. Manakala trek terakhir sama dengan grafik fungsi y = 150 + sin (x). Tetapi dalam program, arah gandar y bertentangan. Jadi, berbanding grafik asal, trek akan terbalik. Sekarang, saya rasa anda pasti mempunyai perasaan bahawa beberapa soalan sukar yang dihantui dalam jangka masa yang lama dapat diselesaikan dengan segera. Sungguh mengagumkan bahawa fungsi hebat ini yang kita pelajari sebelum ini dapat digunakan untuk mengawal pergerakan grafik!
Langkah 2: Untuk Menulis Fungsi
Saya telah menyenaraikan beberapa fungsi yang sering digunakan di bawah. Semoga ini dapat membantu kita menerjemahkan fungsi menjadi kod yang dapat dikenali oleh komputer.
Oleh itu, formula di bawah program ditulis seperti ini:
y = x² → y = pow (x, 2) atau y = sq (x)
y = x³ → y = pow (x, 3)
y = xⁿ → y = pow (x, n)
y = 4ⁿ → y = pow (4, n)
y = logₑ² → y = log (2)
y = e² → y = exp (2)
y = √5 → y = sqrt (5)
Anda juga boleh menulis fungsi secara rawak ke dalam program dan melihat seperti apa trek pergerakannya. Ingatlah untuk mempertimbangkan julat bidang nilai dan domain definisi, atau grafik anda akan habis dari skrin anda.
Fungsi Trigonometrik
Sekarang, mari kita pergi lebih jauh untuk mengetahui beberapa penulisan fungsi trigonometri.
Kita harus memperhatikan bahwa dalam program input parameter fungsi relatif terhadap sudut menggunakan radian. Oleh itu sin90 ° akan ditulis menjadi sin (PI / 2). Sekiranya anda tidak biasa dengan kaedah ini, anda boleh menggunakan randian fungsi untuk mengubah sudut menjadi radian terlebih dahulu, dan kemudian menulis sinian radian (90)).
Penggunaan darjah fungsi agak berlawanan. Ia dapat mengubah radian menjadi sudut. Masukkan cetakan (darjah (PI / 2)) terus ke kawasan edit, dan lihat apa yang anda akan dapat.
Langkah 3: Kawal Pergerakan Grafik Dengan Fungsi Trigonometri
Berikut adalah kes untuk anda melihat kesan sebenar pergerakan grafik.
[cceN_cpp tema = "fajar"] terapung x, y; persediaan tidak sah () {saiz (700, 300); } undian tidak sah () {latar belakang (234, 113, 107); y = sin (radian (x)) * 150 + 150; x ++; noStroke (); elips (x, y, 50, 50); } [/cceN_cpp]
Fungsi sin adalah fungsi berkala. Nilai minimumnya adalah -1, dan nilai maksimum adalah 1. Ketinggian skrin adalah 300. Merujuk kepada y = sin (radian (x)) * 150 + 150, oleh itu julat perubahan nilai y akan dikendalikan dengan baik dalam 0 hingga 300.
Bulatan Berputar
Baiklah, akhirnya kita masuk ke bahagian paling penting dalam bab ini. Bagaimana melukis jalur bulatan dalam program? Bagaimana menggunakan fungsi untuk memaparkannya? Izinkan saya menunjukkan dua gambar yang kami lihat pada awal artikel ini lagi.
Sebenarnya mereka secara visual telah mendedahkan hubungan antara koordinat lilitan dan fungsi trigonometri. Pergerakan dalam gambar di atas didorong oleh pemboleh ubah bebas yang sentiasa meningkat. Kiri adalah gambaran fungsi sin dan kos, dan kanan bermaksud titik yang melakukan pergerakan bulat setelah dipetakan. Bukankah sangat pintar? Ia tidak misteri lagi. Anda boleh menggunakan kod untuk merealisasikannya.
Contoh mudah:
[cceN_cpp tema = "fajar"] apungan x, y, r, R, sudut; batal persediaan () {saiz (300, 300); r = 20; // Diameter bulatan R = 100; // Radius jalur pergerakan x = 0; sudut = 0; y = tinggi / 2; } undian tidak sah () {latar belakang (234, 113, 107); terjemahkan (lebar / 2, tinggi / 2); // Pindahkan titik asal ke pusat skrin. noStroke (); x = R * cos (sudut); y = R * sin (sudut); elips (x, y, r, r); sudut + = 0.05; } [/cceN_cpp]
Lihat! Bulatan berputar muncul! Di sini, pemboleh ubah bebas tidak lebih dalam peningkatan bit terus menjadi sudut (sama dengan θ dalam gambar). Ia bermaksud sudut. Di antaranya, xy mempunyai pekali R yang berlipat ganda, yang membawa kepada perpanjangan radius pergerakan bulatan (R adalah untuk jejari). Sekiranya tidak mengalikan R, jalan pergerakannya akan terhad dalam lingkungan dari -1 hingga 1.
Mengapa tidak menggunakan x yang semakin meningkat? Mengikut sifat fungsi itu sendiri, setiap x dalam domain definisi mempunyai satu-satunya y yang sesuai dengannya. Oleh itu, dalam sistem koordinat dimensi segi empat tepat satah, anda tidak dapat mengetahui "fungsi sederhana" untuk melukis bulatan secara langsung. Maksudnya kita tidak dapat menggunakan format ini lagi.
y = (Ungkapan x yang tidak diketahui?);
x ++;
Oleh itu, kita harus mengubah idea kita. Pilih sudut lain sebagai pemboleh ubah bebas, dan kemudian gunakan fungsi sin dan kos untuk mengubahnya menjadi koordinat mendatar dan menegak.
x = R * cos (sudut);
y = R * sin (sudut);
sudut + = 0.05;
Sebilangan daripada anda mungkin tertanya-tanya mengapa ia dapat menunjukkan jalan pergerakan bulatan. Mengikut definisi fungsi trigonometri, kita dapat dengan mudah mengetahui bahawa fungsi tersebut merupakan nisbah sisi yang berlawanan dengan hipotenus; fungsi cos adalah nisbah berdekatan dengan hipotenus. Di mana pun titik bulatannya, r (jejari) tidak akan berubah. Oleh itu kita dapat membuat kesimpulan ungkapan koordinat x dan koordinat y.
Kerana ini bukan panduan matematik, di sini saya akan berhenti memaparkan lebih banyak pengetahuan mengenai fungsi trigonometri kepada anda. Sekiranya anda ingin mengetahuinya atau anda hanya melupakannya, anda boleh mencubanya sendiri.
Sudah tentu, tidak mengapa jika anda tidak dapat memahaminya sepenuhnya. Anda hanya perlu tahu cara menggunakannya untuk melukis bulatan. Ini juga sejenis "idea pengaturcaraan". Nanti, kita akan sering menggunakan beberapa modul yang ada yang dibuat oleh orang lain untuk merealisasikan jenis fungsi tertentu. Jangan memaksa diri untuk mengetahui secara terperinci.
Walau bagaimanapun, fungsi sin dan cos adalah perkara biasa. Sekiranya anda ingin membuat penciptaan peringkat yang lebih tinggi, lebih baik anda mencuba untuk mengetahui secara menyeluruh. Sekiranya soalan ini sendiri dapat mendorong kita untuk mempelajari lebih banyak pengetahuan matematik, ada lebih banyak perkara menarik yang menanti anda mencuba.
Ini adalah gambar yang berkait rapat dengan fungsi trigonometri.
Langkah 4: Sistem Koordinat Pergerakan
Kesan sebelumnya adalah mengenai perubahan koordinat grafik. Sistem koordinat itu sendiri statik. Sebenarnya kita dapat membuat koordinat bergerak untuk mewujudkan kesan motif. Ini seperti orang-orang di pantai memerhatikan orang lain di dalam kapal. Bagi orang yang menaiki kapal, kapal itu statik. Tetapi bagaimana jika kapal itu sendiri bergerak, maka orang-orang di dalam kapal bergerak dengannya. Kes-kes yang pertama adalah mengenai "orang yang berlari di atas kapal". Sebenarnya, kapal tidak bergerak. Berikut adalah beberapa fungsi umum untuk mengubah sistem koordinat.
Fungsi menterjemahkan
Fungsi terjemahan, yang telah kita bicarakan sebelumnya, digunakan untuk menggerakkan sistem koordinat grafik secara mendatar.
Format panggilan:
terjemahkan (a, b)
Parameter pertama bermaksud bergerak ke arah positif gandar x untuk piksel. Parameter kedua bermaksud bergerak ke arah positif gandar y untuk b piksel.
Bandingkan kedua-dua kod tersebut dan cuba cari perbezaannya. (Untuk mempermudah kod, kita dapat menghapus ukuran fungsi, lebar dan tinggi layar secara default menjadi 100.)
Sebelum kita menggunakan:
elips (0, 0, 20, 20);
Selepas kami menggunakan:
terjemahkan (50, 50);
elips (0, 0, 20, 20);
Fungsi berpusing
Format panggilan:
putar (a)
Ia digunakan untuk sistem koordinat berputar. Apabila parameter positif, ia akan memilih titik asal sebagai titik tengah dan berputar mengikut arah jam. Input parameter sama dengan fungsi trigonometri untuk menggunakan radian.
Sebelum digunakan:
elips (50, 50, 20, 20);
Selepas digunakan:
putar (radian (30));
elips (50, 50, 20, 20);
Kesan dalam program adalah menjadikan bulatan berputar di sekitar titik pusat koordinat mengikut arah pusingan jam selama 30 darjah.
Skala fungsi
Format panggilan:
skala (a)
Fungsi ini dapat memperkecil sistem koordinat. Nilainya adalah untuk penskalaan. Apabila parameter melebihi 1, kemudian zum masuk; jika lebih rendah daripada 1, maka zum keluar.
Sebelum digunakan:
elips (0, 0, 20, 20);
Selepas digunakan:
skala (4);
elips (0, 0, 20, 20);
Lingkaran pada gambar di atas diperbesar hingga empat kali dari ukuran asal. Anda juga boleh menggunakan dua parameter untuk memperkecil arah gandar x dan gandar y secara berasingan.
skala (4, 2);
elips (0, 0, 20, 20);
Superposisi Fungsi Transformasi
Di sini, superposisi adalah mengenai perubahan yang berkaitan dengan sistem koordinat sekarang. Dengan kata lain, kesan boleh ditumpangkan.
terjemahkan (40, 10);
terjemahkan (10, 40);
elips (0, 0, 20, 20);
Kesan akhirnya akan sama dengan
terjemahkan (50, 50);
elips (0, 0, 20, 20);
Sama dengan fungsi putar
putar (radian (10));
putar (radian (20));
elips (50, 50, 20, 20);
Sama dengan
putar (radian (30));
elips (50, 50, 20, 20);
Kedua-dua skala fungsi dan putaran berpusat pada titik asal untuk skala dan berputar. Sekiranya kita ingin mendapatkan kesan putaran dengan kedudukan tengah pada (50, 50), kita harus berfikir dengan cara yang bertentangan. Mula-mula gerakkan titik asal ke kedudukan (50, 50), kemudian tambahkan fungsi transformasi berputar. Akhirnya buat grafik anda dilukis pada titik asal.
Sebelum digunakan:
elips (50, 50, 50, 20);
Selepas digunakan:
terjemahkan (50, 50);
putar (radian (45));
elips (0, 0, 50, 20); // Untuk melihat perubahan sudut putaran, kami telah membuat lonjong.
Mungkin kelihatan berpusing. Anda hanya perlu berlatih lebih banyak maka anda akan memahaminya. (Anda juga boleh cuba mengubah urutan terjemahan fungsi dan memutar untuk melihat perbezaannya.)
Pergerakan Mendatar dan Pergerakan Bulat
Dalam kes-kes berikut, kita akan mewujudkan kesan gerakan dengan mengubah sistem koordinat. Pada masa yang sama, saya ingin meminta anda merujuk kepada contoh bab sebelumnya. Sebilangan besar masa, anda akan dapati untuk mengetahui kesan tertentu, anda boleh menggunakan kaedah yang sama sekali berbeza.
Langkah 5: Pergerakan Mendatar
[cceN_cpp tema = "fajar"]
int x, y; batal persediaan () {saiz (300, 300); x = 0; y = tinggi / 2; } undian tidak sah () {latar belakang (234, 113, 107); noStroke (); terjemahkan (x, y); elips (0, 0, 50, 50); x ++; } [/cceN_cpp]
Koordinat bulatan tidak diubah tetapi sistem koordinatnya diubah.
Putar Pergerakan
[cceN_cpp tema = "fajar"] float r, R, sudut; batal persediaan () {saiz (300, 300); r = 20; // Dimensi bulatan R = 100; // Radius trek pergerakan} undian kosong () {latar belakang (234, 113, 107); terjemahkan (lebar / 2, tinggi / 2); // Pindahkan titik asal ke pusat skrin. putar (sudut); noStroke (); elips (0, R, r, r); sudut + = 0.05; } [/cceN_cpp]
Bukankah lebih jelas dan sederhana daripada fungsi trigonometri? Anda mungkin mempunyai soalan di sini. Ambil kod berputar sebagai contoh. Jelas, fungsi transformasi yang disebutkan di atas adalah relatif dan memungkinkan superimposisi. Sekiranya kita menulis terjemahkan (lebar / 2, tinggi / 2) ke dalam cabutan fungsi, bukankah ini bermaksud setiap kali cabutan fungsi beroperasi sekali, sistem koordinat akan bergerak jarak ke arah bawah kanan dari pangkalan asal? Secara munasabah ia tidak akan kekal di tengah-tengah skrin selama-lamanya.
Anda boleh faham dengan cara ini. Setelah kod dalam fungsi fungsi selesai operasi dari atas ke bawah, sistem koordinat akan kembali ke status awal pada operasi kedua. Titik asal sistem koordinat akan lalai untuk kembali ke sudut kiri atas. Oleh itu, jika kita ingin membuat sistem koordinat berubah secara berterusan, parameter sudut dalam fungsi berputar akan sentiasa meningkatkan nilainya.
Akses Status Koordinat
Kadang-kadang, kita tidak mahu perubahan status sistem koordinat berdasarkan yang sebelumnya. Pada masa ini, kita harus menggunakan fungsi pushMatrix dan popMatrix. Kedua-dua fungsi biasanya muncul dalam pasangan. Fungsi pushMatrix adalah sebelum popMatrix. Mereka tidak boleh digunakan semata-mata, atau ia akan menjadi salah.
Contoh:
[cceN_cpp tema = "fajar"] pushMatrix (); // Terjemahkan status sistem koordinat (50, 50); elips (0, 0, 20, 20); popMatrix (); // Baca kedudukan sistem koordinat tepat (0, 0, 20, 20); [/cceN_cpp]
Dalam contoh ini, sebelum menggunakan translate (50, 50), kita menggunakan fungsi pushMatrix.untuk menyimpan status sistem koordinat semasa. Ini, pada masa yang sama, adalah status awal. Setelah kita melukis bulatan, kemudian melaksanakan popMatrix, ia akan kembali ke status ini. Pada masa ini, laksanakan fungsi fungsi, anda akan mendapati ia tidak mengalami pengaruh fungsi terjemahan sebaliknya melukis segi empat di sudut kiri atas titik asal.
Selain itu, fungsi pushMatrix dan popMatrix membolehkan bersarang.
Sebagai contoh
pushMatrix ();
pushMatrix ();
popMatrix ();
popMatrix ();
Untuk menunjukkan hubungannya secara intuitif, kami memilih format pemeluwapan.
Gabungan Pergerakan atau Pergerakan dalam Pergerakan?
Sekarang gelombang kedua bahagian penting bermula. Cuba terus maju. Sebelum ini, kita telah menggunakan metafora perahu dan orang. Pernahkah anda berfikir tentang bagaimana jika kita membuat orang dan perahu bergerak, perasaan apa yang akan ada di pantai?
Seperti menggabungkan pergerakan mendatar dengan pergerakan sistem koordinat berputar. Maksudnya di sini adalah untuk bergerak ke arah sahaja.
[cceN_cpp tema = "fajar"] int x, y; sudut apungan; batal persediaan () {saiz (300, 300); latar belakang (234, 113, 107); noStroke (); x = 0; // Apabila nilai awal x adalah 0, kita dapat mengabaikan kalimat kalimat ini. Apabila menyatakan pemboleh ubah, nilai lalai adalah 0. y = 0; // Sama seperti di atas. sudut = 0; // Sama dengan perkara di atas. } undian tidak sah () {sudut + = 0.25; y--; terjemahkan (lebar / 2, tinggi / 2); pushMatrix (); putar (sudut); elips (x, y, 5, 5); popMatrix (); } [/cceN_cpp]
Dan terdapat pergerakan pekeliling dan penskalaan sistem koordinat.
[cceN_cpp tema = "fajar"] terapung x, y, sudut; batal persediaan () {saiz (300, 300); latar belakang (234, 113, 107); noStroke (); } undian batal () {sudut + = 0.01; x = sin (sudut) * 100; y = cos (sudut) * 100; terjemahkan (lebar / 2, tinggi / 2); pushMatrix (); skala (1 + 0.1 * sin (sudut * 10)); elips (x, y, 5, 5); popMatrix (); } [/cceN_cpp]
Jangan ditipu olehnya! Titik bulatan sebenarnya melakukan pergerakan bulat. Tidak sukar untuk difahami jika kita membandingkannya dengan penskalaan dengan kamera video. Kamera video bergerak ke hadapan atau ke belakang secara berterusan memotret titik dalam gerakan bulat.
Terkejut? Ini adalah fungsi asas yang mudah. Tetapi dengan kombinasi yang berbeza, kita dapat menghasilkan banyak kesan yang berbeza. Hingga kini, pendedahan saya berhenti sehingga ada ruang untuk penerokaan anda.
Langkah 6: Penggunaan Komprehensif
Ini akan segera berakhir untuk bab ini. Dua bab terakhir, saya telah memperkenalkan kaedah asas pergerakan grafik. Saya percaya anda mungkin mempunyai pemahaman yang lebih mendalam untuknya, berbanding dengan idea awal anda. Paling tidak, berikut adalah beberapa contoh lengkap untuk rujukan anda.
[cceN_cpp tema = "fajar"] terapung x1, y1, x2, y2, r, R; sudut apungan1, sudut2; batal persediaan () {saiz (300, 300); r = 12; R = 120; sudut1 = 0; sudut2 = PI / 4; } undian tidak sah () {latar belakang (234, 113, 107); noStroke (); terjemahkan (lebar / 2, tinggi / 2); sudut1 + = 0.02; sudut2 + = 0.06; x1 = R * sin (sudut1); y1 = R * cos (sudut1); x2 = R / 2 * sin (sudut2); y2 = R / 2 * cos (sudut2); elips (x1, y1, r / 2, r / 2); elips (x2, y2, r, r); elips (-x1, -y1, r / 2, r / 2); elips (-x2, -y2, r, r); elips (x1, -y1, r / 2, r / 2); elips (x2, -y2, r, r); elips (-x1, y1, r / 2, r / 2); elips (-x2, y2, r, r); strok (255); berat badan (3); garis (x1, y1, x2, y2); garis (-x1, -y1, -x2, -y2); garis (x1, -y1, x2, -y2); garis (-x1, y1, -x2, y2); } [/cceN_cpp]
Contoh ini tidak mengandungi pengetahuan selain bab sebelumnya yang diperkenalkan.
Untuk mata yang manakah sesuai? Garisan yang manakah sesuai? Saya juga tidak dapat mengetahuinya. Tetapi saya ingat ia berasal dari bahagian kecil kod.
Inilah sifat pergerakannya. Garisan selebihnya hanya kesan cermin. Sekiranya anda terus mengikuti panduan ini, anda boleh membuat versi terkini dan menambahkan alat kawalan ke grafik anda untuk mengubah status pergerakan grafik anda dalam masa nyata.
Titik pengaturcaraan yang menarik adalah bahawa anda boleh merancang atau menggabungkan peraturan. Walau bagaimanapun, apa yang akan menjadi program akhir semuanya bergantung pada kemampuan anda. Biasanya pereka mempunyai imaginasi grafik yang kuat. Anda boleh melakarkan gambar di kepala anda, dan kemudian cuba menerjemahkannya menjadi kod. Anda juga boleh bermula dari kod dan peraturan itu sendiri, fungsi reka bentuk dan pemboleh ubah sesuka hati. Ingatlah bahawa Memproses adalah lakaran anda dan kod adalah berus anda! Cubalah idea anda dengan bebas!
Langkah 7: TAMAT
Terakhir dalam bab kami, mari kita kembali ke soalan yang telah lama kita simpan sejak awal. Apa gunanya menghabiskan banyak usaha untuk membuat gambar dengan program? Setelah anda mempelajari bab ini, anda akan dapati terdapat banyak kaedah bermain yang menanti anda meneroka.
[cceN_cpp tema = "fajar"] float browX, earD, eyeD, faceD; batal persediaan () {size (500, 500); } undian tidak sah () {latar belakang (200, 0, 0); browX = 150 + sin (frameCount / 30.0) * 20; earD = 180 + sin (frameCount / 10.0) * 20; eyeD = 60 + sin (frameCount / 30.0) * 50; mukaD = 300; berat badan (8); elips (175, 220, earD, earD); elips (lebar - 175, 220, earD, earD); tepat (100, 100, faceD, faceD); garis (browX, 160, 220, 240); garis (lebar-alisX, 160, lebar-220, 240); isi (rawak (255), rawak (255), rawak (255)); elips (175, 220, eyeD, eyeD); elips (lebar-175, 220, eyeD, eyeD); isi (255); titik (lebar / 2, tinggi / 2); segi tiga (170 - cos (frameCount / 10.0) * 20, 300 - sin (frameCount / 10.0) * 20, lebar - (170 + cos (frameCount / 10.0) * 20), 300 + sin (frameCount / 10.0) * 20, 250, 350); } [/cceN_cpp]
Bukankah ini ajaib untuk grafik dinamik? Di sini saya tidak menunjukkan banyak kes. Anda mungkin dapat merancang kesan yang jauh lebih baik daripada saya. Kelebihan melukis dengan program ada anda boleh bermain dengan setiap piksel. Oleh kerana grafik anda bukan peta bit, setiap titik utama pada grafik anda dapat dikawal. Ia dapat menyedari beberapa kesan yang tidak dapat disedari oleh perisian lain.
Sekiranya anda mempunyai hati yang ingin memecahkan semuanya dan menggabungkannya semula, program pengajian akan sangat membantu anda memenuhi idea ini.
Artikel ini berasal dari pereka Wenzy.
Langkah 8: Bacaan Relatif:
Panduan Pengaturcaraan Menarik untuk Pereka - Memproses Sentuhan Awal
Panduan Pengaturcaraan Menarik untuk Pereka - Buat Program Pemprosesan Pertama Anda
Panduan Pengaturcaraan Menarik untuk Pereka - Menjalankan Gambar Anda (Bahagian Pertama)
Sekiranya anda mempunyai sebarang pertanyaan, anda boleh menghantar e-mel ke [email protected].
Artikel ini berasal dari:
Disyorkan:
Panduan Pengaturcaraan Pemprosesan Menarik untuk Pereka - Kawalan Warna: 10 Langkah

Panduan Pengaturcaraan Pemrosesan yang Menarik untuk Pereka - Pengawalan Warna: Pada bab-bab sebelumnya, kita telah membincangkan lebih banyak mengenai cara menggunakan kod untuk melakukan pembentuk dan bukannya titik pengetahuan mengenai warna. Dalam bab ini, kita akan meneroka aspek pengetahuan ini dengan lebih mendalam
Panduan Berjalan untuk Meningkatkan Mobiliti Orang Cacat Penglihatan: 6 Langkah
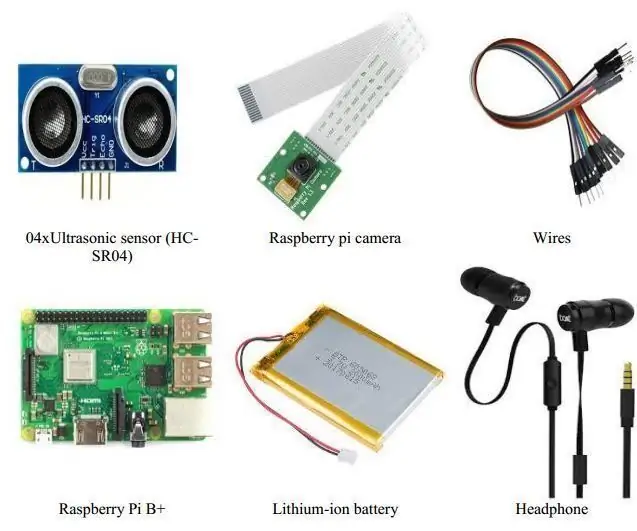
Panduan Berjalan untuk Meningkatkan Mobiliti Orang yang Bermasalah Penglihatan: Matlamat yang boleh dipelajari adalah untuk mengembangkan panduan berjalan yang boleh digunakan oleh orang kurang upaya, terutamanya orang yang cacat penglihatan. Pengajar bermaksud untuk menyiasat bagaimana panduan berjalan dapat digunakan dengan berkesan, sehingga keperluan reka bentuk
Panduan Pengaturcaraan Pemprosesan Menarik untuk Pereka - Pemuatan dan Acara Media: 13 Langkah

Panduan Pengaturcaraan Pemrosesan Menarik untuk Pereka - Pemuatan dan Acara Media: Pemprosesan dapat memuat banyak data luaran, di antaranya terdapat tiga jenis yang sangat biasa digunakan. Mereka adalah gambar, audio dan video secara berasingan. Dalam bab ini, kita akan membincangkan bagaimana memuatkan audio dan video secara terperinci, menggabungkan dengan acara
Panduan Pengaturcaraan Menarik untuk Pereka - Kawalan Proses Program- Pernyataan Gelung: 8 Langkah

Panduan Pengaturcaraan Menarik untuk Pereka - Pengendalian Proses Program- Pernyataan Gelung: Kawalan Proses Program- Pernyataan GelungDari bab ini, anda akan berhubung dengan Pernyataan Loop-titik pengetahuan yang penting dan kuat. Sebelum membaca bab ini, jika anda ingin menarik 10,000 bulatan dalam program ini, anda hanya dapat melakukan
Panduan Pengaturcaraan Menarik untuk Pereka - Menjalankan Gambar Anda (Bahagian Satu): 16 Langkah

Panduan Pengaturcaraan Menarik untuk Pereka - Menjalankan Gambar Anda (Bahagian Satu): Lari! Lari! Jalankan! Pengaturcaraan tidak begitu sukar. Perkara utama adalah mencari irama anda dan melakukannya satu persatu. Sebelum membaca bab ini, saya harap anda sudah biasa dengan kaedah menggambar fungsi asas, atau anda akan merasa pening dan keliru
