
Isi kandungan:
- Langkah 1: Hasilkan Matriks NxN Uniform Square
- Langkah 2: Mengacak Rangkaian
- Langkah 3: Dapatkan Jarak Baru
- Langkah 4: Pilih Titik dan Bandingkan Jarak Dari Titik Itu ke Yang Lain
- Langkah 5: Pindah ke Titik Baru
- Langkah 6: Jarak = K * jarak
- Langkah 7: Ubah Pergerakan Rangkaian Kerana Titik Bergerak
- Langkah 8: Kod Selesai
- Pengarang John Day day@howwhatproduce.com.
- Public 2024-01-30 11:11.
- Diubah suai terakhir 2025-01-23 15:01.

Sel dapat berinteraksi dengan matriks ekstraselular di sekitarnya (ECM) dan boleh berlaku serta bertindak balas terhadap daya yang diberikan oleh ECM. Untuk projek kami, kami mensimulasikan rangkaian gentian yang saling berkaitan yang akan bertindak sebagai ECM dan melihat bagaimana rangkaian berubah sebagai tindak balas terhadap pergerakan salah satu titik. ECM dimodelkan sebagai sistem mata air yang saling berkaitan yang pada awalnya berada pada keseimbangan dengan daya bersih sifar. Oleh kerana daya diterapkan ke jaringan sebagai respons terhadap pergerakan titik, kami berusaha mendapatkan titik-titik yang terhubung untuk bertindak balas terhadap gaya sedemikian rupa sehingga mereka berusaha untuk kembali ke keseimbangan. Daya dipantau oleh persamaan F = k * x di mana k adalah pemalar spring dan x adalah perubahan panjang gentian. Simulasi ini dapat membantu memberikan pemahaman umum mengenai penyebaran daya dalam rangkaian berserat yang akhirnya dapat digunakan untuk menolong mensimulasikan mekanotransduksi.
Langkah 1: Hasilkan Matriks NxN Uniform Square


Untuk memulakan kod, kami memilih N yang akan menentukan dimensi rangkaian kami (NxN). Nilai N dapat diubah secara manual untuk mengubah dimensi rangkaian seperti yang diperlukan. Dalam contoh ini, N = 8 jadi kita mempunyai rangkaian titik 8x8. Selepas kami menghasilkan matriks, kami menyambungkan semua titik dalam matriks yang mempunyai panjang 1 unit menggunakan formula jarak, jarak = sqrt ((x2-x1) ^ 2 + (y2-y1) ^ 2). Dengan melakukan ini, kita mendapat rangkaian kotak yang semuanya jaraknya sama dengan 1 unit. Ini dapat dilihat pada rajah 101.
Langkah 2: Mengacak Rangkaian


Dalam langkah ini, kita ingin mengacak semua lokasi titik kecuali titik luar yang akan membentuk batas kita. Untuk melakukan ini, pertama-tama kita menjumpai semua koordinat matriks yang sama dengan 0 atau N. Titik-titik ini adalah titik yang membentuk sempadan. Untuk titik bukan sempadan, lokasi secara rawak dengan menambahkan nilai rawak yang berbeza dari -.5 hingga.5 ke kedua-dua kedudukan x dan y. Gambar rawak yang diplot dapat dilihat pada Gambar 1.
Langkah 3: Dapatkan Jarak Baru

Setelah rangkaian rawak kami dibuat, kami dapati jarak antara titik bersambung menggunakan formula jarak lagi.
Langkah 4: Pilih Titik dan Bandingkan Jarak Dari Titik Itu ke Yang Lain



Pada langkah ini, kita dapat memilih tempat menarik menggunakan kursor, seperti yang ditunjukkan pada Gambar 2. Anda tidak perlu menggerakkan kursor tepat ke titik tersebut kerana kod akan menyesuaikannya ke titik sambungan terdekat. Untuk melakukan ini, pertama-tama kita mengira jarak antara semua titik bersambung dan titik yang baru kita pilih. Setelah semua jarak dikira, kami memilih titik dengan jarak terkecil dari titik yang dipilih untuk menjadi titik terpilih yang sebenarnya.
Langkah 5: Pindah ke Titik Baru



Pada langkah ini, menggunakan titik yang dipilih pada langkah sebelumnya, kita memindahkan titik ke lokasi baru. Pergerakan ini dilakukan dengan memilih kedudukan baru dengan kursor yang akan menggantikan kedudukan sebelumnya. Pergerakan ini akan digunakan untuk mensimulasikan daya yang diberikan kerana perubahan panjang musim bunga. Dalam semua gambar biru, lokasi baru sedang dipilih. Pada gambar berikutnya, pergerakan dapat dilihat dengan sambungan oren yang merupakan lokasi baru berbanding dengan sambungan biru yang merupakan lokasi lama.
Langkah 6: Jarak = K * jarak

Dalam langkah ini kita menerapkan daya persamaan = k * jarak, di mana k adalah pemalar 10 untuk serat kolagen. Oleh kerana rangkaian gentian bermula pada keadaan keseimbangannya, daya bersih adalah 0. Kami membuat vektor sifar panjang matriks yang kami hasilkan sebelumnya untuk mewakili keseimbangan ini.
Langkah 7: Ubah Pergerakan Rangkaian Kerana Titik Bergerak




Dalam langkah ini, kita mensimulasikan pergerakan rangkaian sebagai tindak balas terhadap pergerakan titik untuk kembali ke keadaan keseimbangannya. Kita mulakan dengan mencari jarak baru antara dua titik. Dengan ini kita dapat mengetahui perubahan panjang serat dengan melihat perbezaan jarak lama dan baru. Kita juga dapat melihat titik mana yang telah berpindah dan juga titik yang dihubungkan dengan membandingkan lokasi titik baru dan lama. Ini membolehkan kita melihat titik mana yang harus bergerak sebagai tindak balas terhadap kekuatan yang diberikan. Arah pergerakan dapat dipecah menjadi komponen x dan y, memberikan vektor arah 2D. Dengan menggunakan nilai k, perubahan jarak, dan vektor arah, kita dapat mengira vektor daya yang dapat digunakan untuk menggerakkan titik kita ke arah keseimbangan. Kami menjalankan bahagian kod ini 100 kali, setiap kali bergerak dengan kenaikan Force *.1. Menjalankan kod 100 kali membolehkan kita akhirnya mencapai keseimbangan lagi dan dengan menjaga keadaan sempadan, kita melihat perubahan dalam rangkaian dan bukannya hanya pergeseran keseluruhan. Pergerakan rangkaian dapat dilihat pada Gambar 3 dengan warna kuning menjadi posisi bergerak dan biru menjadi yang sebelumnya.
Langkah 8: Kod Selesai
Di bahagian ini terdapat salinan kod kami. Jangan ragu untuk mengubahnya agar sesuai dengan keperluan anda dengan memodelkan pelbagai rangkaian!
Disyorkan:
Jauh Lampu Luar Luar 10W RGB: 5 Langkah

10W RGB Outside Night Lamp Remote: Projek ini adalah lampu LED 10GB RGB untuk malam, ia boleh diletakkan di sebelah anda dan memberi anda suasana suasana berjam-jam. Saya terinspirasi oleh Lampu Balad yang terdapat di Perancis tetapi agak kuat (versi komersialnya kira-kira 3W, lombong 10W) dan banyak lagi
Membuat Grafik Perubahan Suhu Dari Perubahan Iklim di Python: 6 Langkah
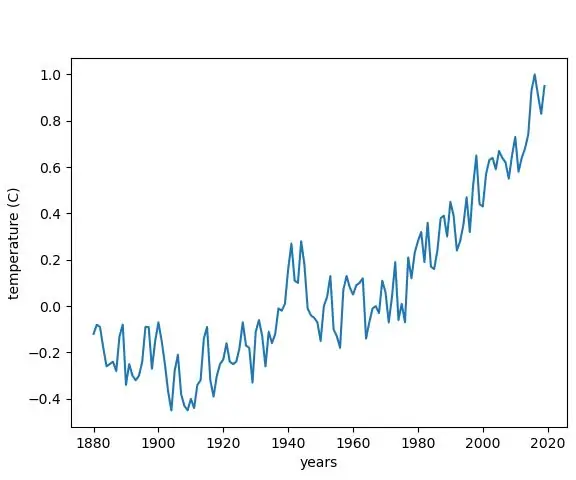
Menggambarkan Perubahan Suhu Dari Perubahan Iklim di Python: Perubahan Iklim adalah masalah besar. Dan banyak orang sekarang tidak berapa jumlahnya meningkat. Dalam instruksional ini, kami akan membuat grafik perubahan suhu dalam iklim kerana perubahan iklim. Untuk cheat sheet, anda boleh melihat fail python di bawah
Jam yang Jatuh Dari Tembok Apabila Anda Melihatnya: 4 Langkah

Jam yang Jatuh Dari Tembok Ketika Anda Melihatnya: Pernahkah anda menginginkan jam yang tidak memberitahu anda masa. Saya tidak, tetapi itulah yang anda dapat apabila anda memasukkan saya ke dalam karantina dengan beberapa komponen elektronik, dan internet
Penjaga Kata Laluan pada Aruino Pro Micro atau Mengapa Tetap Mudah Apabila Cara yang Ringkas Ada !: 15 Langkah (dengan Gambar)

Penjaga Kata Laluan pada Aruino Pro Micro atau Mengapa Tetap Ringkas Ketika Cara yang Ringkas Ada !: Nampaknya, masalah utama dengan mikrokontroler untuk peminat elektronik (terutamanya pemula) adalah untuk mengetahui di mana menerapkannya :) Elektronik sekarang, terutamanya digital , semakin kelihatan seperti ilmu hitam. Hanya petua 80-Lvl yang
Apa yang Perlu Dilakukan Apabila ITunes Tidak Mengenali IPod Anda: 7 Langkah

Apa yang Perlu Dilakukan Apabila ITunes Tidak Mengenali IPod Anda: Oleh itu, anda menerima iPod baru anda dan anda sangat teruja untuk menggunakannya. Anda pasangkan kabel USB ke komputer dan pasangkan hujung yang lain ke iPod anda. Sekarang anda menghadapi masalah. Atas sebab tertentu iTunes tidak mengesan iPod anda. Anda mungkin menganggap ini adalah pr
