
Isi kandungan:
- Pengarang John Day day@howwhatproduce.com.
- Public 2024-01-30 11:07.
- Diubah suai terakhir 2025-01-23 15:00.


Berikut adalah aplikasi praktikal persamaan matematik kompleks.
Ini sebenarnya teknik yang sangat berguna yang dapat anda gunakan untuk mencirikan komponen, atau bahkan antena, pada frekuensi yang telah ditentukan.
Sekiranya anda bermain-main dengan elektronik, anda mungkin biasa dengan Resistor dan undang-undang Ohm.i. R = V / I Anda sekarang mungkin terkejut apabila mengetahui ini yang perlu anda selesaikan untuk masalah impedans yang rumit juga! Semua impedans pada dasarnya kompleks, iaitu, mereka mempunyai bahagian Nyata dan Khayalan. Dalam kes Resistor, khayalan (atau reaktansi) adalah 0, dan tidak ada perbezaan fasa antara V dan I, sehingga kita dapat meninggalkannya.
Ringkasan ringkas mengenai nombor kompleks. Kompleks bermaksud bilangannya terdiri daripada dua bahagian, yang nyata dan yang khayalan. Ada dua cara untuk mewakili nombor kompleks, misalnya pada gambar di atas, titik dapat ditentukan oleh nilai Nyata dan Imajiner, seperti di mana garis kuning dan biru bertemu. Sebagai contoh jika garis biru berada pada 4 pada paksi X, dan 3 pada paksi Y, nombor ini akan menjadi 4 + 3i, saya menunjukkan bahawa ini adalah bahagian khayalan nombor ini. Cara lain untuk menentukan titik yang sama adalah dengan panjang (atau amplitud) garis merah serta sudut apa yang dibuat dengan garis mendatar. Dalam contoh di atas ini akan menjadi 5 <36.87.
Atau garis dengan panjang 5 pada sudut 36.87 darjah.
Dalam persamaan di atas semua parameter, R, V dan I dapat dianggap mempunyai bahagian khayalan, ketika bekerja dengan perintang nilai ini adalah 0.
Semasa bekerja dengan induktor atau kapasitor, atau ketika perbezaan fasa dapat diukur (dalam darjah) antara isyarat, persamaannya tetap sama tetapi bahagian khayalan nombor mesti disertakan. Sebilangan besar kalkulator saintifik menjadikan kerja dengan matematik kompleks sangat mudah, dalam tutorial ini saya akan bekerja melalui contoh pada Casio fx-9750GII.
Pertama, rangkuman pada persamaan pembahagi voltan perintang.
Seperti rajah -
Voltan pada Y adalah arus saya didarab dengan R2
i ialah voltan X dibahagi dengan jumlah R1 dan R2
Apabila R2 tidak diketahui, kita dapat mengukur nilai lain, X, Y, R1 dan menyusun semula persamaan untuk menyelesaikan R2.
Bekalan
Kalkulator saintifik
Penjana isyarat
Osiloskop
Langkah 1: Persediaan

Anggaplah kita mahu mengira induktansi Peranti Dalam Uji (DUT) pada 1MHz.
Penjana isyarat dikonfigurasikan untuk output sinusoidal 5V pada 1MHZ.
Kami menggunakan perintang 2k ohm, dan saluran osiloskop adalah CH1 dan CH2
Langkah 2: Osiloskop

Kami mendapat bentuk gelombang seperti yang ditunjukkan dalam gambar. Peralihan fasa dapat dilihat dan diukur pada osiloskop untuk dipimpin oleh 130ns. Amplitudinya ialah 3.4V. Perhatikan, isyarat pada CH1 harus 2.5V kerana diambil pada output pembahagi voltan, di sini ditunjukkan sebagai 5V untuk kejelasan, kerana ini adalah nilai yang juga harus kita gunakan dalam pengiraan kita. 5V adalah voltan masukan ke pembahagi dengan komponen yang tidak diketahui.
Langkah 3: Kira Fasa

Pada 1MHz tempoh isyarat input adalah 1us.
130ns memberikan nisbah 0.13. Atau 13%. 13% daripada 360 adalah 46.6
Isyarat 5V diberi sudut 0.. kerana ini adalah isyarat input kami dan pergeseran fasa relatif terhadapnya.
isyarat 3.4V diberi sudut +46.6 (+ bermaksud ia mengarah, untuk kapasitor sudut akan negatif).
Langkah 4: Pada Kalkulator


Sekarang kita memasukkan nilai yang diukur ke dalam kalkulator.
R ialah 2k
V adalah 5 (EDIT - V adalah 5, kemudian dalam persamaan digunakan X! Hasilnya sama seperti saya mempunyai X sebagai 5 dalam kalkulator saya)
Y adalah voltan yang diukur dengan sudut fasa, nombor ini dimasukkan sebagai nombor kompleks, hanya dengan menentukan sudut seperti yang ditunjukkan pada skrin kalkulator
Langkah 5: Selesaikan Persamaan

sekarang persamaannya
(Y * R) / (X - Y)
ditaip ke dalam kalkulator, ini adalah persamaan yang sama dengan yang kita gunakan untuk menyelesaikan pembahagi voltan perintang:)
Langkah 6: Nilai yang Dikira


Kalkulator menghasilkan hasilnya
18 + 1872i
The 18, adalah bahagian sebenar dari impedans dan ia mempunyai induktansi +1872 pada 1MHz.
Yang berfungsi hingga 298uH mengikut persamaan impedans induktor.
18 ohm lebih tinggi daripada rintangan yang akan diukur dengan multimeter, ini kerana multimeter mengukur rintangan pada DC. Pada 1MHz terdapat kesan kulit, di mana bahagian dalam konduktor dipintas oleh arus dan hanya mengalir di bahagian luar tembaga, dengan berkesan mengurangkan luas silang konduktor, dan meningkatkan daya tahannya.
Disyorkan:
Jam Pelangi Matematik-Fizik: 3 Langkah (dengan Gambar)
Jam Pelangi Matematik-Fizik: Beberapa ketika dahulu saya mempunyai idea untuk membuat jam Fizik / Matematik sendiri, jadi saya mula merancangnya di Inkscape. Setiap jam, dari 1 hingga 12, saya digantikan dengan formula Fizik / Matematik: 1 - Persamaan Euler2 - Integral 3 - Fungsi trigonometri4 - Integral trigonom
Komponen Kompleks Desoldering: 4 Langkah

Komponen Kompleks Desoldering: Adakah anda pernah mahu mengeluarkan cip atau komponen rawak dari papan litar rawak yang anda miliki? Pasti itu mudah dilakukan dengan perkara seperti kapasitor atau LED, tetapi apabila berkaitan dengan perkara yang lebih kompleks, ia akan menjadi lebih sukar. … Dan apabila keadaan menjadi
Menggunakan Papan Sensor Seni Kompleks untuk Mengawal Data Murni Melalui WiFi: 4 Langkah (dengan Gambar)

Menggunakan Papan Sensor Seni Kompleks untuk Mengawal Data Murni Melalui WiFi: Adakah anda pernah ingin bereksperimen dengan kawalan isyarat? Buat perkara bergerak dengan gelombang tangan anda? Kawal muzik dengan sentuhan pergelangan tangan anda? Instructable ini akan menunjukkan kepada anda bagaimana! Dewan Seni Sensor Kompleks (complexarts.net) adalah mikrok
Menjana Nada Jenis Berbeza Menggunakan Persamaan Matematik (MathsMusic) Arduino: 5 Langkah

Menjana Nada Jenis Berbeza Menggunakan Persamaan Matematik (MathsMusic) Arduino: Penerangan Projek: Perjalanan baru telah bermula di mana idea dapat dilaksanakan dengan mudah menggunakan komuniti sumber terbuka (Terima kasih kepada Arduino). Jadi, inilah caranya · Lihat sekeliling anda dan perhatikan persekitaran anda · Cari Masalah yang perlu
Mengukur Impedansi Menggunakan LTspice: 4 Langkah
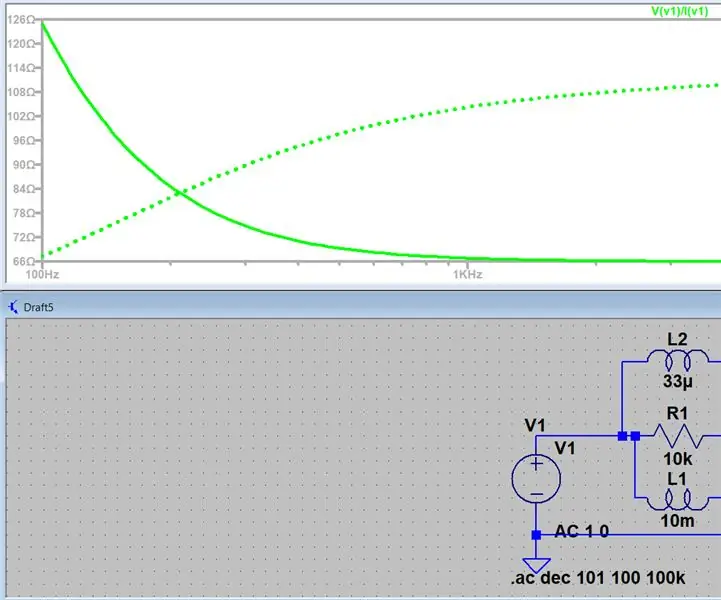
Mengukur Impedansi Menggunakan LTspice: Hai semua ini akan menjadi pengenalan mudah untuk menghasilkan sapuan litar AC dan mencari galangan pada titik tertentu, ini muncul beberapa kali dalam kursus saya dan sangat sukar bagi saya untuk mencari cara melakukannya dalam talian jadi
