Isi kandungan:
- Langkah 1: Memahami Jadual Kebenaran
- Langkah 2: Mengetahui Simbol
- Langkah 3: Memformat Jadual
- Langkah 4: Menetapkan Betul dan Salah
- Langkah 5: Negasi
- Langkah 6: Pemboleh ubah "q"
- Langkah 7: Selesaikan untuk Salah di Lajur Terakhir
- Langkah 8: Mencari Benar di Lajur Terakhir
- Langkah 9: Menyelesaikan Jadual
- Langkah 10: Selesai
- Pengarang John Day [email protected].
- Public 2024-01-30 11:07.
- Diubah suai terakhir 2025-01-23 15:00.

Jadual kebenaran adalah cara untuk memvisualisasikan semua hasil masalah. Set arahan ini dibuat untuk orang yang memulakan matematik diskrit. Kami akan berlatih hari ini dengan contoh masalah yang khusus untuk arahan ini. Anda memerlukan sedikit kertas calar dan pensil untuk menggambarkan jadual. Masalah ini memerlukan masa sekitar 5 minit untuk diselesaikan bagi orang yang mempunyai pengetahuan sebelumnya mengenai topik tersebut dan sekitar 10 minit untuk pemula.
Untuk set arahan ini, kami akan memfokuskan pada masalah ~ p Λ q. Kami menggunakan ini untuk memperkenalkan beberapa simbol yang diperlukan untuk menafsirkan jadual kebenaran.
Langkah 1: Memahami Jadual Kebenaran

Jadual kebenaran adalah cara untuk memvisualisasikan semua kemungkinan masalah. Mengetahui jadual kebenaran adalah keperluan asas untuk matematik diskrit. Di sini, kita akan menemui semua hasil untuk persamaan mudah ~ p Λ q.
Langkah 2: Mengetahui Simbol

Langkah pertama menuju jadual kebenaran adalah memahami tanda-tandanya. “~” Dalam masalah ini bermaksud penolakan. The "p" dan "q" adalah kedua-dua pemboleh ubah. “Λ” setara dengan “dan”. Persamaan ini dibaca sebagai "bukan p dan q", yang bermaksud, persamaan itu benar jika p tidak benar dan q adalah benar.
Langkah 3: Memformat Jadual

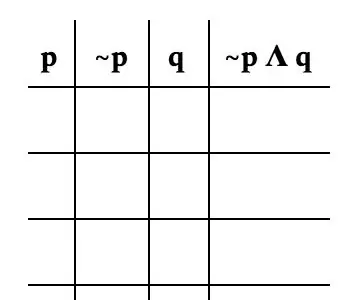
Sekarang untuk membentuk jadual sebenar. Penting untuk mengatasi masalah oleh setiap pemboleh ubah. Untuk masalah ini, kita akan memecahkannya seperti berikut: p, ~ p, q, dan ~ p Λ q. Imej adalah contoh yang baik dari rupa jadual anda.
Langkah 4: Menetapkan Betul dan Salah

Oleh kerana hanya ada dua pemboleh ubah, hanya akan ada empat kemungkinan setiap pemboleh ubah. Untuk p, kami membahagikannya dengan separuh ruang yang diambil oleh T (untuk true) dan separuh lagi dengan F (untuk false).
Langkah 5: Negasi

Untuk ~ p, anda menuliskan tanda bertentangan bahawa p mempunyai ~ p adalah kebalikan dari p.
Langkah 6: Pemboleh ubah "q"

Untuk q, anda bergantian antara T dan F untuk mendapatkan setiap kemungkinan kombinasi. Oleh kerana persamaan hanya tertumpu pada ~ p, kita boleh mengabaikan lajur p ketika menentukan kebenaran persamaan. Simbol "Λ" bermaksud kedua-dua ~ p dan q harus benar agar persamaan itu benar.
Langkah 7: Selesaikan untuk Salah di Lajur Terakhir

Untuk baris pertama, kerana ~ p adalah F dan q adalah T, ~ p Λ q adalah F dalam senario yang ~ p adalah F dan q adalah T. Satu-satunya senario persamaannya adalah T adalah di mana ~ p adalah T dan q adalah T.
Langkah 8: Mencari Benar di Lajur Terakhir

Ini bermaksud satu-satunya baris yang adalah T adalah baris ketiga.
Langkah 9: Menyelesaikan Jadual

Periksa semula bahawa jadual anda betul. Anda melakukan ini dengan memeriksa tanda anda betul dan memastikan lajur terakhir dilakukan dengan betul. Lajur terakhir adalah hasil semua kemungkinan permutasi dari pemboleh ubah.
Langkah 10: Selesai
Sekarang setelah anda mengetahui cara membuat jadual kebenaran asas, terus berlatih! Semakin banyak anda berlatih, semakin baik anda melakukannya.
Disyorkan:
Cara Membuat dan Memasukkan Jadual dan Menambah Lajur Tambahan dan / atau Baris ke Jadual Itu di Microsoft Office Word 2007: 11 Langkah

Cara Membuat dan Memasukkan Jadual dan Menambah Lajur Tambahan dan / atau Baris ke Jadual Itu di Microsoft Office Word 2007: Pernahkah anda mempunyai banyak data yang anda gunakan dan fikirkan sendiri … " bagaimana saya dapat membuat semua data ini kelihatan lebih baik dan lebih mudah difahami? " Sekiranya demikian, maka jadual di Microsoft Office Word 2007 mungkin adalah jawapan anda
Jadual Jadual: Pembantu Produktiviti Maya Anda: 6 Langkah (dengan Gambar)

Jadual Jadual: Pembantu Produktiviti Maya Anda: Saya seorang penunda profesional! Penguncian ini membuat saya berada dalam lingkaran masa, di mana setiap hari hanya terbang tanpa kerja yang produktif. Untuk mengatasi penundaan saya, saya telah membuat jam ringkas dan pantas ini, yang menjadualkan kerja saya. Sekarang saya hanya boleh berpegang pada
Cara Menyelesaikan Masalah Peningkatan Pengawal Clone SimpleBGC: 4 Langkah
Cara Menyelesaikan Masalah Peningkatan Pengawal Clone SimpleBGC: Helo. Baru-baru ini, saya bekerja menggunakan pengawal gimbal SimpleBGC untuk projek drone saya. Saya berjaya menyambung dan menyesuaikannya. Ia berfungsi dengan sempurna. Selepas itu, saya mahu menaik taraf firmware dari v2.2 ke v2.4. Jadi, setelah saya menaik taraf gimbal itu
Bagaimana Menyelesaikan Masalah Reka Bentuk PCB?: 8 Langkah (dengan Gambar)

Bagaimana Mengatasi Masalah Reka Bentuk PCB ?: Setiap kali saya merancang PCB, saya ingin sedikit had saya dan mencuba sesuatu yang tidak pernah saya cuba sebelumnya, kali ini saya ingin menambah kemungkinan untuk memprogram papan ini tanpa pengaturcara luaran. Saya menjumpai beberapa penukar USB ke UART yang murah yang dipanggil CH
Menyelesaikan Pekerjaan: Memasang Papan Kekunci USB ke dalam Laptop OLO XO, Tahap II: 6 Langkah

Menyelesaikan Pekerjaan: Memasang Papan Kekunci USB ke dalam Laptop OLPC XO, Fasa II: Untuk seorang lelaki yang menghabiskan sebahagian besar hidupnya dengan jari-jarinya yang tersambung ke baris rumah, menambahkan papan kekunci USB ini yang benar-benar dapat saya sentuh-jenis telah membuat perbezaan besar dalam kebolehgunaan XO. Ini adalah " fasa II " - memasang insi kabel
